ZKpuzzle::0CTF 2025

(Updated: )

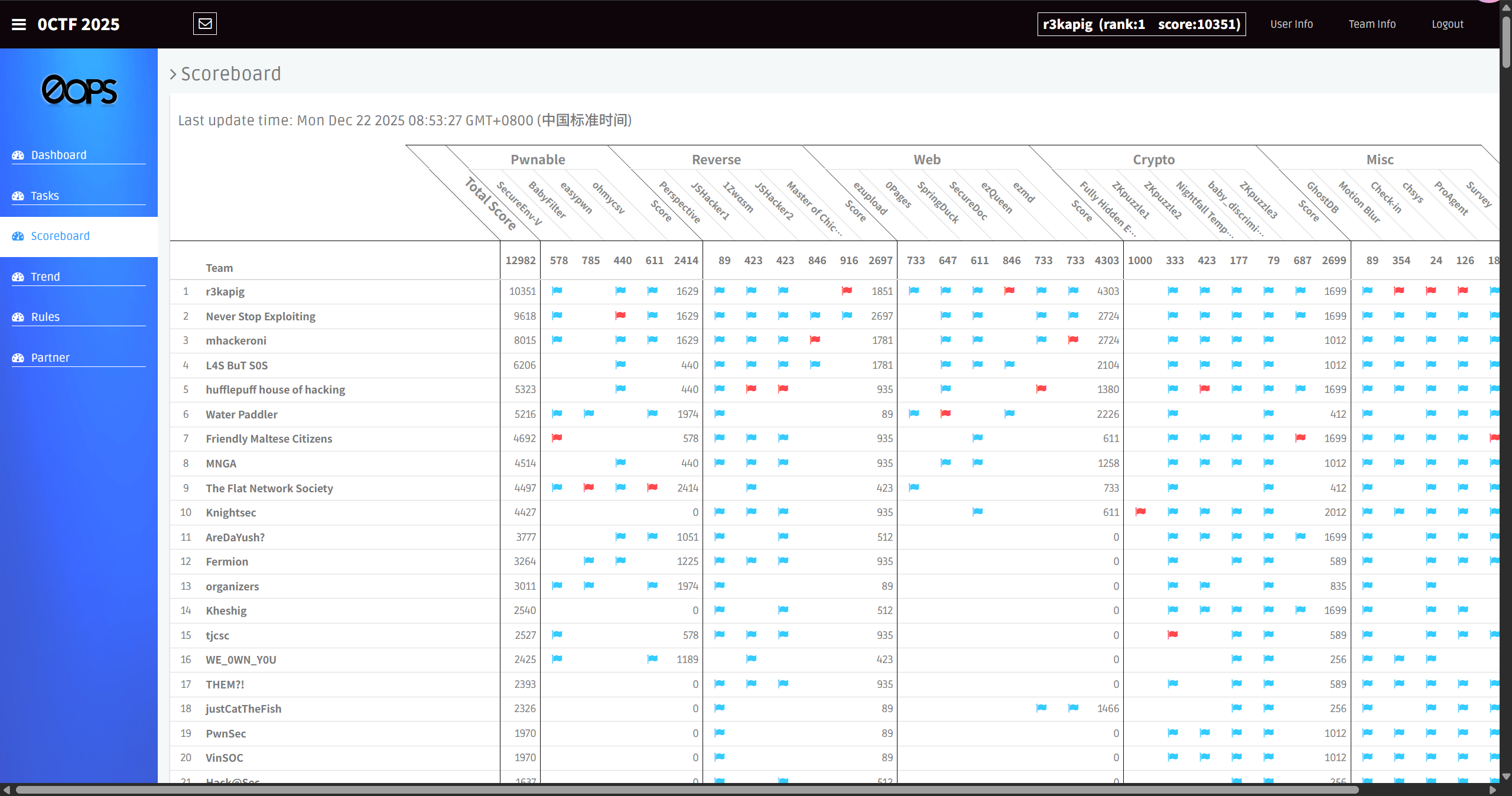
Time: 2025.12.20-21 (online)

I participated in 0CTF 2025 with r3kapig this weekend, we ended up as 1st place gg.

scoreboard

Learned a lot about Sum of Four Cubes Problem this year. (Again, why you call them zkp challenges @sh1k4ku XD)

@deebato so strong

ZKpuzzle

In the following 3 ZKpuzzles, we will deal with Sum of Four Cubes Problem with different constraints.

ZKpuzzle1

In this Stage 1, we’re given two random 128-bit integers $(r, k)$ and we need to find $(w_1, w_2, w_3, w_4)$ satisfying $\Sigma w_i^3 = r \cdot k^3 \pmod{p_1 \cdot p_2}$ and $w_i < 2^{200}$.

Curve Selection

First things first, we need to submit 2 primes and verify the answer on the constructed elliptic curves. However there’s an implicit constraint in the following code:

1
2
3
4
5
6
7
class proofSystem:
    def myrand(self, E1, E2):
        F = Zmod(E1.order())
        r = F.random_element()
        P = r * E2.gens()[0]
        x = P.x()
        return int(r * x) & (2**128 - 1)

It turns out if r and x are not in the same field, the code will crash out at int(r * x). So we need to find a pair of curves $(E_1, E_2)$ satisfying $E_i.p = E_{2-i}.order$.

But we don’t need to face it now. Instead we can set $E_1 = E_2$ and find an anomalous curve with $E.p = E.order$.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sage.all import * 
b = 137

def find_prime_for_anomalous_curve(target_b): 
    y = randrange(2**127,2**128) | 1
    while True:
        #  4p = 1^2 + 3y^2  => p = (3y^2 + 1) / 4
        numerator = 3 * y**2 + 1
        if numerator % 4 == 0:
            p = numerator // 4
            if is_prime(p): 
                try:
                    E = EllipticCurve(GF(p), [0, target_b])
                    if E.order() == p:
                        return p
                except Exception as e: 
                    pass
        y += 2

Our Solution

Now let’s deal with the Sum of Four Cubes part.

Actually we can try to solve $\Sigma w_i^3 = r \cdot k^3 + t \cdot p$ on $\mathbb{Z}$, which is a widely-studied problem. With certain conditions satisfied, we can find the answer through specific constructions; if we can’t find one, we can just try another $t$.

Since many constructions lead to $w_i$ with the same (or bigger) scale as the target, we used the following method during the competition:

$$
(u+v)^3 + (u-v)^3 + (-u+w)^3 + (-u-w)^3 = 6 \cdot u \cdot (v-w) \cdot (v+w)
$$

With an appropriate target, we can pass the 200-bit constraint and solve the challenge.

ZKpuzzle2

In Stage 2, we’re given two random 128-bit integers $(r, k)$, we need to find $(w_1, w_2, w_3, w_4)$ satisfying $\Sigma w_i^3 = r \cdot k^3 \pmod{p_1 \cdot p_2}$ and $w_i < 2^{400}$. But this time, more constraints are added on curve selection.

2-Cycle Curves

Now we need to face the curve problem: we need to find a pair of curves $(E_1, E_2)$ satisfying $E_i.p = E_{2-i}.order$. We also need to control the Hamming weight of the primes which determines our interaction rounds.

With some research, I found out this is a well-known structure called 2-cycle curves, which is widely used in recursive zkSNARKs. And luckily, NTT is a common requirements and a NTT-friendly prime often exhibits specific characteristics in terms of Hamming weight, which precisely suits to the challenge. I just used the generator implmented by Zcash during the competition.

1
2
p   = 0b1100000000110000000000110000000000000000000000000000000000000000000000000000000000000000000000000000000000011000000000110000000000010000100000010000000000000000000000100000100000000000000000001000001000010000000000001100000000001000000000000000000000000001
q   = 0b1100000000110000000000110000000000000000000000000000000000000000000000000000000000000000000000000000000000011000000000110000000110010000101100010000000000000000000000100000100000000000000000000100000100010000000000001100000000000100000110000000000000000001

Our Solution

We can not reuse the method in ZKpuzzle1 because here we need to factor $r \cdot k^3 + t \cdot p_1 \cdot p_2$, which is 512 bit.

But the good news is the limit has been raised up to 400 bit, larger than the 256 bit prime. Can we solve the equation on $\mathbb{F}_p$ and $\mathbb{F}_q$, and then try to combine the results under the limitation?

The answer is yes. First let’s consider the following equation:
$$
(u + a)^3 + (-u)^3 = (3 \cdot u^2 + 3 \cdot u \cdot a + 3 \cdot a^2) \cdot a
$$

We have:
$$
(u + t \cdot p)^3 + (-u)^3 = (3 \cdot u^2 + 3 \cdot u \cdot (t \cdot p) + 3 \cdot (t \cdot p)^2) \cdot t \cdot p = 0 \pmod{p}
$$

So we can construct the equation:
$$
(u + t \cdot p)^3 + (-u)^3 + (v + s \cdot q)^3 + (-v)^3 = r \cdot k^3 \pmod{p \cdot q} \\
\Rightarrow
\left\{
\begin{matrix}
(u + t \cdot p)^3 + (-u)^3 = r \cdot k^3 \pmod{q} \\
(v + s \cdot q)^3 + (-v)^3 = r \cdot k^3 \pmod{p} \\
\end{matrix}
\right.
$$

Then we just pick up some small $(t, s)$ and try to solve $(u, v)$ on $\mathbb{F}_q$ and $\mathbb{F}_p$ separately. We can combine the results to get the final answer (which is 256 bit or so, actually).

ZKpuzzle3

In Stage 3, we’re given a random 128-bit integers $r$, we need to find $(w_1, w_2, w_3, w_4)$ satisfying $\Sigma w_i^3 = r$ and $w_i < 2^{260}$. The curve constraints are the same as Stage 2.

Our Solution

The equation in Stage 2 is still useful, but with a different way:
$$
\begin{aligned}
r &= (u+x)^3 + (-x)^3 + (v+y)^3 + (-y)^3 \\
&= u^3 + v^3 + 3 \cdot u \cdot (u \cdot x + x^2) + 3 \cdot v \cdot (v \cdot y + y^2) \\
&\Rightarrow \\
4 \cdot r &= u^3 + v^3 + 3 \cdot u \cdot (2 \cdot x + u)^2 + 3 \cdot v \cdot (2 \cdot y + v)^2 \\
&\Rightarrow \\
\frac{4 \cdot r - u^3 - v^3}{3} &= u \cdot (2 \cdot x + u)^2 + v \cdot (2 \cdot y + v)^2 \\
&= u \cdot A^2 + v \cdot B^2
\end{aligned}
$$

By doing this, we can transform the original problem into a (Diagonal) Binary Quadratic Form on $\mathbb{Z}$. During the competition we just used BinaryQF(u, 0, v).solve_integer(t) and it worked well, if there exists a solution.

The key point here is that we need wisely pick up $(u, v)$ such that the BQF is solvable. The author @sh1k4ku fixes $u = 1$ and try to solve $A^2 + v \cdot B^2 = t$ for all $v$. Based on experiments, this indeed gives us a slight advantage.

Optimization

There exists several optimizations to pass the 90s limit.

We found this tool. It turns out Sum of Four Cubes Problem has been studied for a long time and a valid answer can be constructed in many conditions. Basically, if $r \neq 4 / 5 \pmod{9}$ we can always find a solution with this tool, which saves us much time.

Another optimization is that since our target is to solve the problem within $\{r, …, r+ROUND\}$, one can precompute all the solutions parallelly once he knows $r$.