BlackHat MEA CTF 2025 Final (Riyadh, Saudi Arabia🇸🇦)

rec

2025-12-09 (Updated: 2025-12-25)

AES, McEliece, SPN

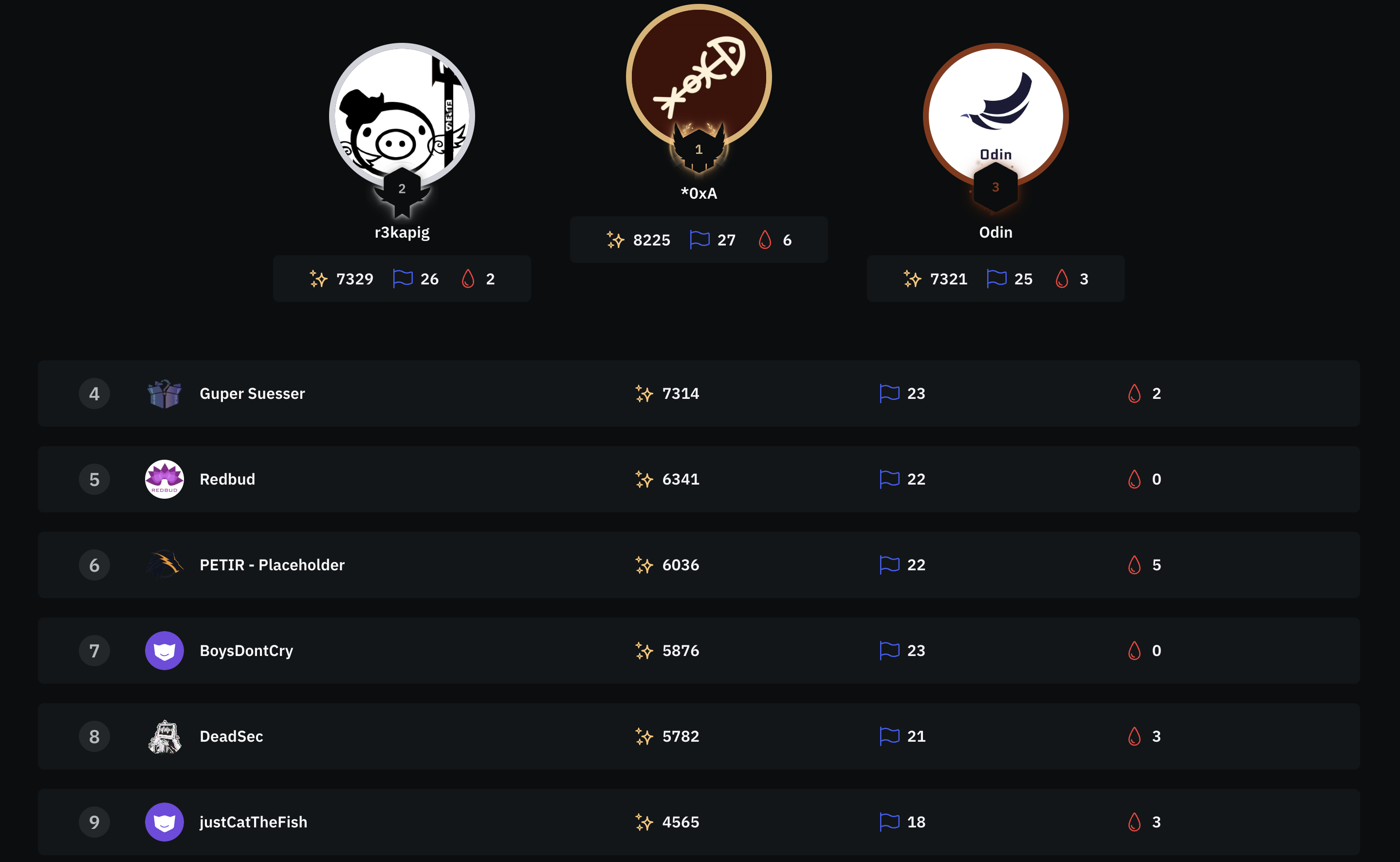
Time: 2025.12.02-04 (onsite)

I attended the Black Hat MEA CTF 2025 Final with r3kapig in Riyadh, Saudi Arabia.

After three days working we got the 2nd place 🥈 in the competition, GG to all my teammates!

scoreboard

day1

Que?

que.py

@chatgpt didn’t get a chance to take a look. XD

Tampering Detection System

server.py

AES-GCM

aes-gcm

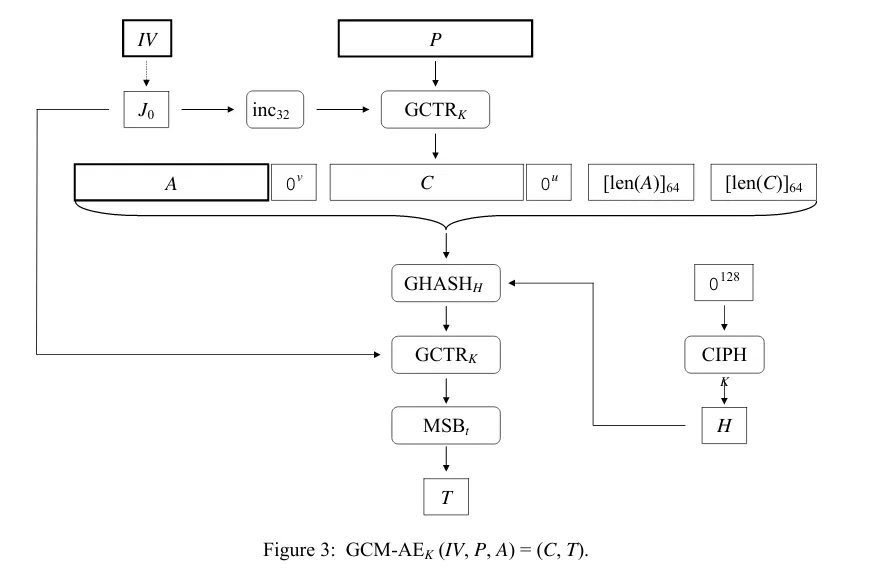
Some code by me for a better understanding. (I prefer $E_0$ while it’s $J_0$ in the figure.)

from sage.all import GF
from Crypto.Util.number import long_to_bytes, bytes_to_long
from Crypto.Cipher import AES


z0 = GF(2)["z0"].gen()
F, z = GF(2**128, name="z", modulus=z0**128 + z0**7 + z0**2 + z0 + 1).objgen()


def xor(a, b):
    return bytes([ai^bi for ai, bi in zip(a, b)])

def pad128(pt):
    return pt + b'\x00' * ((16 - len(pt))%16)

def len64(pt):
    return long_to_bytes(len(pt)*8, 8)

def b2gf(b):
    return F(list(bin(bytes_to_long(b))[2:].zfill(128)))

def gf2b(g):
    return long_to_bytes(int(''.join(map(str, g.list())), 2), 16)


def TAG(key: bytes, aad: bytes, nonce: bytes, ct: bytes):
    aes = AES.new(key=key, mode=AES.MODE_ECB)
    E0 = aes.encrypt(nonce + long_to_bytes(1, 4))
    H = aes.encrypt(long_to_bytes(0, 16))
    C = pad128(aad) + pad128(ct) + len64(aad) + len64(ct)
    TAG = 0
    for i in range(0, len(C), 16):
        TAG += b2gf(C[i:i+16])
        TAG *= b2gf(H)
    TAG += b2gf(E0)
    return gf2b(TAG) # GHASH(H, C) + E0

def CT(key: bytes, nonce: bytes, pt: bytes):
    aes = AES.new(key=key, mode=AES.MODE_ECB)
    H = aes.encrypt(long_to_bytes(0, 16))
    ctr = nonce + long_to_bytes(1, 4)
    ct = b''
    for i in range(0, len(pt), 16):
        ctr = long_to_bytes(bytes_to_long(ctr) + 1, 16)
        pti = pt[i: i+16]
        cti = xor(pti, aes.encrypt(ctr)[:len(pti)])
        ct += cti
    return ct

GCM Routine

As always, we need to recover (H, E0) first. We have:

tag = GHASH(H, C) + E0
tag2 - tag1 = GHASH(H, C2) - GHASH(H, C1) = GHASH(H, xor(C2, C1))

Then we can find the roots of the polynomial on GF, which includes H. We don’t know (ct1, ct2) but for AES-GCM we have xor(ct1, ct2) = xor(pt1, pt2), and xor(C1, C2) = 0_128||xor(pt1, pt2)||0_64||0_64.

With H, we can solve E0 = tag_flag - GHASH(H, C_flag), thus enabling us to forge a valid tag for any ciphertext.

AAD Construction

In the second part we’re given a decryption oracle, requiring truncating length and aad. Our target is to recover ct and decrypt the flag.

One may notice that each ct corresponds to a unique aad, which can be solved from a linear equation on GF. Consider we have recovered ct[:i], we can bruteforce ct[:i+1] = ct[:i] + ch and find the real ch by checking the corresponding aad, thus recovering ct byte by byte.

z0 = GF(2)["z0"].gen()
F, z = GF(2**128, name="z", modulus=z0**128 + z0**7 + z0**2 + z0 + 1).objgen()
x = F["x"].gen()

for ch in range(256):
    aad = b"\x00"*16
    ct = prefix + bytes([ch])
    C = pad128(aad) + pad128(ct) + len64(aad) + len64(ct)
    ftag = 0
    for i in range(0, len(C), 16):
        if i == 0:
            Ci = x
        else:
            Ci = b2gf(C[i: i+16])
        ftag += Ci
        ftag *= b2gf(H)
    ftag += b2gf(E0) + b2gf(tag2)
    ans = ftag.univariate_polynomial().roots()
    aad = gf2b(ans[0][0])

With a long enough ct, we can decrypt our flag now.

exp.py

day2

doloRSitAmet

server.py

All about Sample Strategy

Clearly, 4 equations are not enough to solve the whole system, but we can ‘glue’ some variables by setting certain seeds. For instance we can fix 1,2 showing up together, which leads to a new variable.

At first I tried to split them into 3 parts like [(0), (1,2,3), (4)].

Seed 15901 gives [0, 1, 2, 3, 4]
Seed 22733 gives [4, 1, 2, 3, 0]
Seed 15054 gives [1, 2, 3, 0, 4]
Seed 17502 gives [1, 2, 3, 4, 0]

With 4 equations we can obtain a linear equation of the form $a \cdot x + b \cdot y + c = 0 \pmod{n}$. It’s indeed solvable with LLL, but we need some (too much) luck to get 2 small variables. This costed me a lot of time.

Then I realized if we glue 4 variables together, there’s only 2 variables left in 2 equations, and we can obtain a univariate polynomial. Just do it twice:

Seed 15901 gives [0, 1, 2, 3, 4]
Seed 17502 gives [1, 2, 3, 4, 0]
Seed 4145  gives [0, 2, 3, 4, 5]
Seed 15589 gives [2, 3, 4, 5, 0]

With 2 polynomials, we can solve the first variable by gcd. This gives us another linear equation with 2 variables (the first sentence and the flag sentence) but much smaller (there’s only 32 bytes unknown in the flag sentence), so we just LLL and get the flag.

exp.py

limeade

limeade.py

A juicy challenge, for real.

Structure Analysis

To put it briefly, Lime includes permutation (Roll) and substitution (Squeeze) funcion. And Jucier essentially constructs a 2-round SPN cipher with each round using the same key:

permuted (lime[0]) key addition
16 times substitution (lime[1]) and permutation (lime[2])
permuted (lime[3]) key addition
16 times substitution (lime[4]) and permutation (lime[5])
permuted (lime[6]) key addition

Boomerang Style Attack

We are provided Encryption/Decryption Oracle with additional fault injection on the key. But first let’s think about what we can do with xor fault injection.

An interesting observation is that $P \oplus K = (P \oplus 1) \oplus (K \oplus 1)$, so if we inject 1 bit fault on both the key and the plaintext at the same position, it shows no difference after the first round of encryption. But with the second key addition, the fault will be injected and the final ciphertext goes completely different.

Encryption
↓   P0, K                   →   P0+perm[0](1), K+1

:   P0                      →   P0+perm[0](1)
↓perm[0] key add
:   P0+perm[0](K)           →   P0+perm[0](1)+perm[0](K+1) = P0+perm[0](K)
↓16 sub[1]-perm[2]
:   P1                      →   P1
↓perm[3] key add
:   P1+perm[3](K)           →   P1+perm[3](K+1)
↓16 sub[4]-perm[5]
:   P2                      →   P2'
↓perm[6] key add
:   P2+perm[6](K)           →   P2'+perm[6](K+1)

=   P2+perm[6](K)           →   P2'+perm[6](K+1)

Why don’t we do it again? This time let’s inject on both the key and the ciphertext, and do the decryption.

=   P0+perm[0](1)           →   P0''

:   P0+perm[0](1)           →   P0''
↑perm[0] key add
:   P0+perm[0](K)           →   P0''+perm[0](K)
↑16 sub[1]-perm[2]
:   P1                      →   P1+perm[3](1)
↑perm[3] key add
:   P1+perm[3](K+1)         →   P1+perm[3](K+1)
↑16 sub[4]-perm[5]
:   P2'                     →   P2'
↑perm[6] key add
:   P2'+perm[6](K+1)        →   P2'+perm[6](K)

↑   P2'+perm[6](K+1), K+1   →   P2'+perm[6](K), K
Decryption

This means a lot: now we have a pair of $(P_0, P_0’’)$ which only have 1 bit difference after the first round of encryption. Let take another step forward…

Encryption
↓   P0'', K                 →   P0''+perm[0](1), K+1

:   P0''                    →   P0''+perm[0](1)
↓perm[0] key add
:   P0''+perm[0](K)         →   P0''+perm[0](1)+perm[0](K+1) = P0''+perm[0](K)
↓16 sub[1]-perm[2]
:   P1+perm[3](1)           →   P1+perm[3](1)
↓perm[3] key add
:   P1+perm[3](K+1)         →   P1+perm[3](K+1)+perm[3](K+1) = P1
↓16 sub[4]-perm[5]
:   P2'                     →   P2
↓perm[6] key add
:   P2'+perm[6](K)          →   P2+perm[6](K+1) = P2+perm[6](K)+perm[6](1)

=   P2'+perm[6](K)          →   P2+perm[6](K)+perm[6](1)

Finally, we manage to obtain a ciphertext with 1 bit difference compared to the original one. Based on this we can construct a distinguisher with our additional fault injection:

Encrypt a random plaintext with the original key.
Inject 1 bit additional fault on the i-th bit of the key.
Obtain the magic ciphertext with 1 bit fault injected.

If success, the additional fault on the i-th bit equals to a 1 bit xor fault. For most parts of the key, this implies the i-th bit is 0 (with high probability). Injection on the MSB may always cause 1 bit fault so we need to bruteforce it instead.

exp.py

(*)ella

ella.py

No need for any paper, it’s just parity statistics.

I may spend more time on this challenge later.

day3

NoisyChannel

server.py

Our Solution

It turns out that randbytes is implemented with getrandbits, with MT19937 as the prng core.

# random.py

def randbytes(self, n):
    """Generate n random bytes."""
    return self.getrandbits(n * 8).to_bytes(n, 'little')

Our target is to find a kernel vector that can be used for any random seeds. If this is even possible, it implies we are dealing with a non-full-rank linear system. Therefore, we can randomly generate sets of data, concatenate them, and then extract a non-trivial vector from its left kernel space as the answer.

exp.py

(*)LCC LLC

Here comes a McEliece challenge.

Decode Failure Oracle

Core functions below.

The server uses McEliece to generate access tokens, and our target is to forge a valid token with admin privilege.

class McEliece(BinaryGoppaCode):
    def Encrypt(self, msg: bytes, eloc: List[int] = None) -> bytes:
        """ Encrypts a message. """
        assert 8 * len(msg) <= self.k
        mvec = Bytes2BitVec(msg, self.k)
        if eloc is None:
            evec = self._RandomMaxWeight()
        else:
            evec = Matrix(GF(2), [1 if i in eloc else 0 for i in range(self.n)])
        cvec = mvec * self.maskedG + evec
        return BitVec2Bytes(cvec)
    
    def Decrypt(self, cip: bytes) -> Tuple[bytes, set]:
        """ Decrypts a ciphertext. """
        assert len(cip) <= -(-self.n // 8)
        cvec = Bytes2BitVec(cip, self.n)
        mvec, evec = self.DecodeCodeWord(cvec * self.Pinv)
        eloc = set([i for i,j in enumerate((evec * self.P).list()) if j])
        return BitVec2Bytes(mvec * self.Sinv), eloc

class LCC:
    def GenerateToken(self, username: str, admin: bool = False) -> str:
        """ Generates a token. """
        salt = os.urandom(24)
        token = json.dumps({
            'username' : username,
            'admin' : admin,
            'salt' : B64Encode(salt)
        }).encode()
        timestamp, eloc, etag = self.HashErrorLocs(salt)
        encToken = self.code.Encrypt(token, eloc)
        return '.'.join(B64Encode(i) for i in [timestamp, salt, etag, encToken])
    
    def LoadToken(self, token: str) -> dict:
        """ Loads a token. """
        try:
            timestamp, salt, etag, encToken = [B64Decode(i) for i in token.split('.')]
            decToken, eloc = self.code.Decrypt(encToken)
            loadedToken = json.loads(decToken.strip(b'\0'))
        except:
            raise ValueError('Failed to load token...')
        # _, _eloc, _etag = self.HashErrorLocs(salt, timestamp)
        try:
            # assert _eloc == eloc
            # assert _etag == etag
            assert salt == B64Decode(loadedToken['salt'])
        except:
            raise ValueError('Invalid token...')
        return loadedToken

# Homepage
@app.route('/', methods=['GET'])
def index():
    token = request.cookies.get('token')
    if token:
        try:
            userData = lcc.LoadToken(token)
            flash('Succesfully loaded your token.', 'success')
            if userData['admin'] == True:
                content = FLAG.decode()
            else:
                content = 'Nothing to see here. Where you looking for something?'
            return render_template(
                'index.html',
                username = ' ' + userData['username'],
                content = content
            )
        except ValueError as e:
            flash('ERROR:: {}'.format(str(e)), 'error')
        except Exception as e:
            print('ERROR:: {}'.format(str(e)))
            flash('Something went wrong...', 'error')
    else:
        flash('No token found. Get a token by visiting "./gettoken/<username>".', 'warning')
    return render_template('index.html', username='', content='Please load your token or generate a new one.')

There’s not so much we can do actually, since we’re only provided with some partly controllable tokens (even without the public key).

You can notice that LoadToken does not check eloc or etag, which may lead to something interesting. For McEliece, Decrypt works if there’re less than t positions of errors. This means if we inject 1 more bit error into a token, it will not be decoded successfully. But if we inject noise again at a “dirty” position, the effects of the noise will be cancelled out and it still serves as a valid token (again, because eloc is not checked).

So we can flip each bit of the token and try to decode it. By checking the response status, we can leak the “dirty” bits of the token, thus recovering a “clean” McEliece token. This gives us some advantages to forge new tokens based on the existing ones: if one tries to do so with “dirty” tokens (i.e. linear combinations), noise accumulation will make it unusable. “NOT CLEAN ENOUGH”

Optimization

For one token recovery, we need n times interactions, which costed 20~30 minutes during the competition. Parallelization should be a good strategy in flask but it didn’t work due to some deployment issues. This took all my time during the competition and it’s kinda disappointing actually…still cool challenge though :D

Another optimization is that we can flip 2 bits at one time:

2 “clean” bits: the token will be rejected since there’re t+2 “dirty” bits.
1 “clean” bit and 1 “dirty” bit: the token will be accepted since there’re still t “dirty” bits.
2 “dirty” bits: the token will be accepted since there’re t-2 “dirty” bits.

By doing this n/2 times, we can ambiguously locate each “dirty” bits. With another 2*t (less than this actually) checks and we can recover the exact eloc.

JSON Manipulation

Let’s delve deeper into this challenge. It may be a choice to recover the public key with enough “clean” tokens, which enables us to forge any valid tokens. But it requires too much interactions.

Since we can control the username part of the token, it can be optimized with some JSON tricks. But first we need to make something clear.

You may notice that json works a little different on the server. This is because app.json instead of json will be called when flask.app is working, which will sort the keys first before serializing a JSON object.

a = {"username": "", "admin": False, "salt": ""}


import json
json.dumps(a)
# {"username": "", "admin": false, "salt": ""}


from flask import app
app = Flask(__name__)
app.json.sort_keys
# True
app.json.dumps(a)
# {"admin": false, "salt": "", "username": ""}
app.json.sort_keys = False
app.json.dumps(a)
# {"username": "", "admin": false, "salt": ""}

In this case, we are enabled to manipulate JSON by constructing a malicious username. For instance:

username = '","admin":true,"salt":"'
a = '{"admin": false, "salt": "", "username": "$"}'.replace("$", username)
json.loads(a)
# {'admin': True, 'salt': '', 'username': ''}

By doing this we can 1) set admin to True and 2) set salt to a valid B64 string (an empty string here).

We can not do this directly, however. Instead we should construct 3 usernames satisfying xor(a, xor(b, c)) = target, and xor the corresponding tokens together. With high probability, we can get a valid token (since we need the salt part to be valid as well). Here we only need 2 “clean” tokens to make the result token accepted.

In Saudi Arabia

Still can’t believe we did it, my teammates are so strong. Got some luck too I guess.

Met so many old and new friends here, enjoyed.

But 3-day competition is really tiring and we didn’t have so much time or energy to travel around. Will do more exploitation in the city if I come next year.