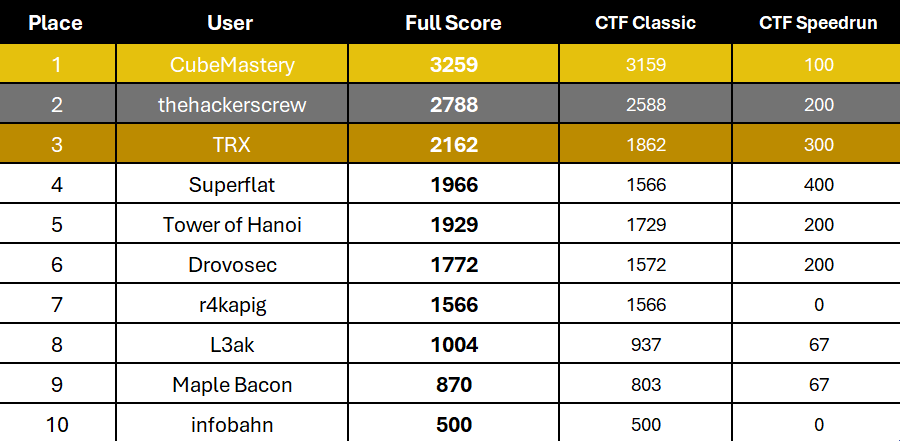
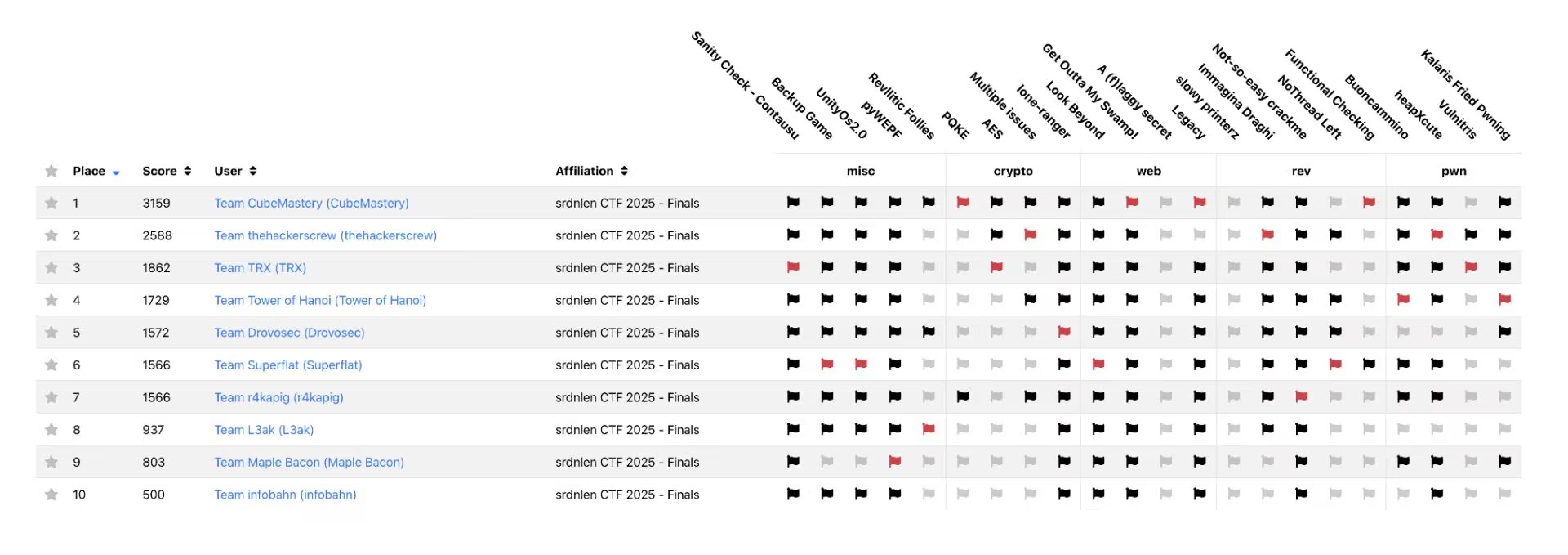
Time: 2025.09.25-26 (onsite)
I attended the first Srdnlen CTF Final with r3kapig, and we ended up as rk7.
We really enjoyed the whole event, sincere thanks to all srdnlen fellas :D
lone-ranger (10 solves)
People solving this challenge insanely fast, so we assumed it’s easier than it looks like. Then gpt-5 cooked the challenge in minutes.
I should still go through the whole challenge later, maybe.
multiple-issues (4 solves)
In this challenge we need to forge a valid UOV signature with a 256-time oracle.
Vuln
Let’s take a deeper look into the funciton sign:
1 | class UOV: |
If we can find two signatures with the same $v$ but different $o$, we can extract a vector $o \in \mathcal{O}$. So the core idea is to find the collision of self.expand_from_seed(self.sigma + msg + int_to_bytes(k), (self.n,)).
An interesting fact is int_to_bytes(0) = ''. Suppose we have msg0 and msg1 = msg0+int_to_bytes(k0). If we have:
v0 = expand(sigma+msg0+int_to_bytes(k))aborts atk = k0.v1 = expand(sigma+msg1+int_to_bytes(k))aborts atk = 0.
This constructs a collision:
v1 = expand(sigma+msg1+'') = expand(sigma+msg0+int_to_bytes(k0)) = v0.
Our strategy is to set a random msg[0] and let msg[i+1] = msg[i] + int_to_bytes(1) (you can also use other k). The collision will take place when msg[i] aborts at k = 1, and msg[i+1] aborts at k = 0. You can find the answer with the fact that $\mathcal{O}$ is the kernel space of the public key.
Solution
For convenience, I may use quadratic mapping style expression:
- $\mathcal{P}_i(v) = v \cdot P_i \cdot v$.
- $\mathcal{P}_i’(v_i, v_j) = v_i \cdot P_i \cdot v_j$.
With a single nontrivial vector $o \in \mathcal{O}$ leaked, we can recover the whole kernel space $\mathcal{O}$. For this part, we used Hellman’s writeup.
The general idea is to extract the kernel space of $\mathcal{K} = \ker(\{ o \cdot P_i \}_i)$ first, where $\dim(\mathcal{K}) = n-m$. Here we have $\mathcal{P}_i(v) = 0$ for any $v \in \mathcal{K}$. This also works for $\mathcal{O}$ but stronger: we have $\mathcal{P}_i’(v_i, v_j) = 0$ for any $v_i, v_j \in \mathcal{O}$. So $\mathcal{O} \subset \mathcal{K}$ and $\dim(\mathcal{O}) = m$.
Consider the basis set $\mathcal{K} = \operatorname{span}(K_{n, n-m})$ and $\mathcal{O} = \operatorname{span}(O_{n, m})$. We can always find a linear transformation $B_{n-m, m}$ s.t. $O = K \cdot B$. Then we have $O^T \cdot P_i \cdot O = B^T \cdot (K^T \cdot P_i \cdot K) \cdot B = 0$, and we can extract such $B$ from $\ker(K^T \cdot P_i \cdot K)$, thus recovering the whole $\mathcal{O}$.
pqke (2 solves)
In this challenge we need to crack a MLWE-based KE scheme.
Tricky Trick
The parameters used in this challenge is slightly weaker than Kyber256 (consider RLWE in Kyber512), with a larger modulus $q = 65537$. But this still does NOT give us enough advantage to solve the RLWE.
The key part of this challenge is a tricky way to generate uniform polynomials:
1 | class Ring: |
The challenge use binomial to generate small polynomials, the same way as in Kyber and Dilithium. But it calls binomial first and use the evaluations to generate uniform polynomials. This means the evaluations of the uniform polynomial $f(x_i)$ on the NTT points $x_i$ are small. If the evaluation $f(x_i) = 0$ (with a non-negligible probability), $f$ contains $(x-x_i)$ as a factor, which serves as a common factor with $x^n+1 = \Pi_i (x - x_i)$.
Based on experiments, we can get a 45-degree common factor on average.
Solution
What can we do with this? Basically we can use the common factors to eliminate some variables and leak information about the others.
Consider a single part of the MLWE as a RLWE instance: $b(x) = s_0(x) \cdot m_0(x) + s_1(x) \cdot m_1(x) + e(x) \pmod{x^n+1}$. Let $g_{0, 1}(x) = \gcd(m_0(x), m_1(x), x^n+1)$, we have $b(x) = e(x) \pmod{g_{0, 1}(x)}$, which leads to a easier scenario (compared to the original one). And we can solve $e(x)$ with lattice reduction if the degree of $g(x)$ is big enough.
Then we can solve the secret polynomials $(s_0(x), s_1(x))$ with $e(x)$. This time we use $g_0(x) = \gcd(m_0(x), x^n + 1)$, and $b(x) - e(x) = s_1(x) \cdot m_1(x) \pmod{g_0(x)}$. Now we can solve $s_1(x)$ (and $s_0(x)$ similarly).
(*)aes (3 solves)
In this challenge we need to crack a cursed AES with a decryption oracle.
Cursed Key Expansion
Apart from the cipher structure, the main change in the challenge is expand_key, with a strange series of sboxes. It can be noticed that the new sboxes contain several n-to-1 mappings. With deeper experiments, we found that this leads to the round keys gradually converging to a fixed value.
Converging to the love for Sardinia, yay.
1 | from server import AES |
The 6 round still has uncertainties, but it converges with an acceptable probability (1/1024 approximately). This gives us a chance to extract a 4-round AES-style cipher from the original one. With a decryption oracle, square attack is a good choice.
I didn’t have time to implement the attack when I figured it out, however.
4-Round Square Attack
For this attack you may find this helpful. The last time I implemented the attack was in 2023, for Blocky challenges in PBCTF and 0CTF.
In square attack we need a $\Lambda$-set, like [bytes([i] + [0]*15) for i in range(256)], where all elements have only one different byte. An interesting fact is that sub_bytes and add_round_key does not disrupt the structure of the set, while mix_columns combined with shift_rows does.
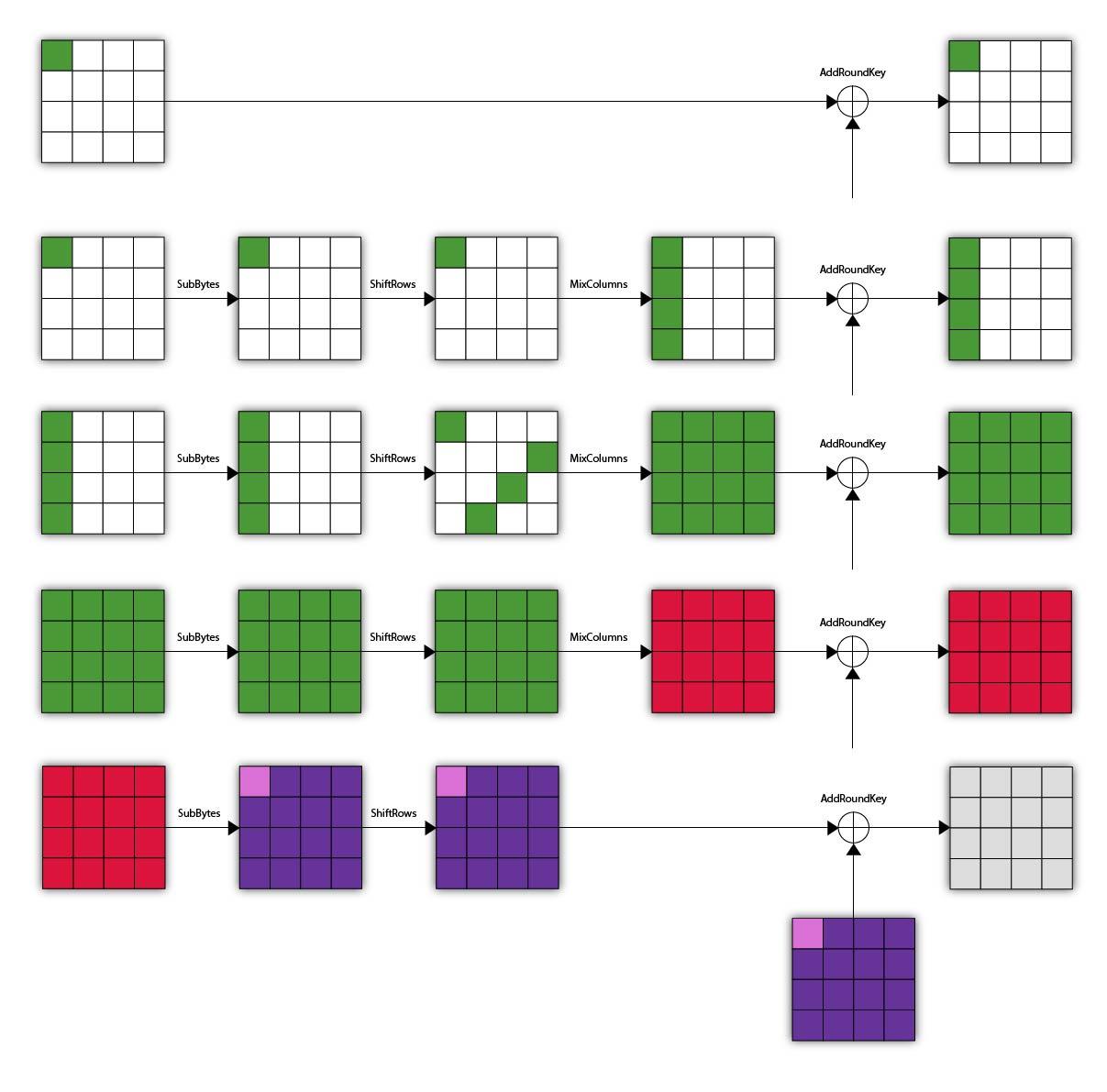
Let’s conduct a brief analysis on how the $\Lambda$-set changes (with this famous and clear flowchart by david). At the very beginning, there’s only one active byte. After the first mix_columns, the corresponding bytes in the other rows also get activated. And with the effect of shift_rows, the next mix_columns makes it even more chaotic.
After the third mix_columns, our $\Lambda$-set does not exist anymore, but our adventure’s not over yet. At this point, each byte of the element is a linear combination of 4 previous active bytes, and we can get a linear combination of 4 zero if we sum them up (for “sum them up” I mean pt[0][i] ^ pt[1][i]...).
The core of the attack is the fact that, the phenomenon described above provides us a key distinguisher.
The following add_round_key does not change anything, but after sub_byte things will be different. For each byte of the last round_keys[-1] we can bruteforce it, step back to before the last sub_bytes, and recover round_keys[-1] by checking whether the property of the $\Lambda$-set holds. People should know that this is a parallel-friendly strategy.
5-Round Square Attack
One more round added, but there’re no significant changes actually.
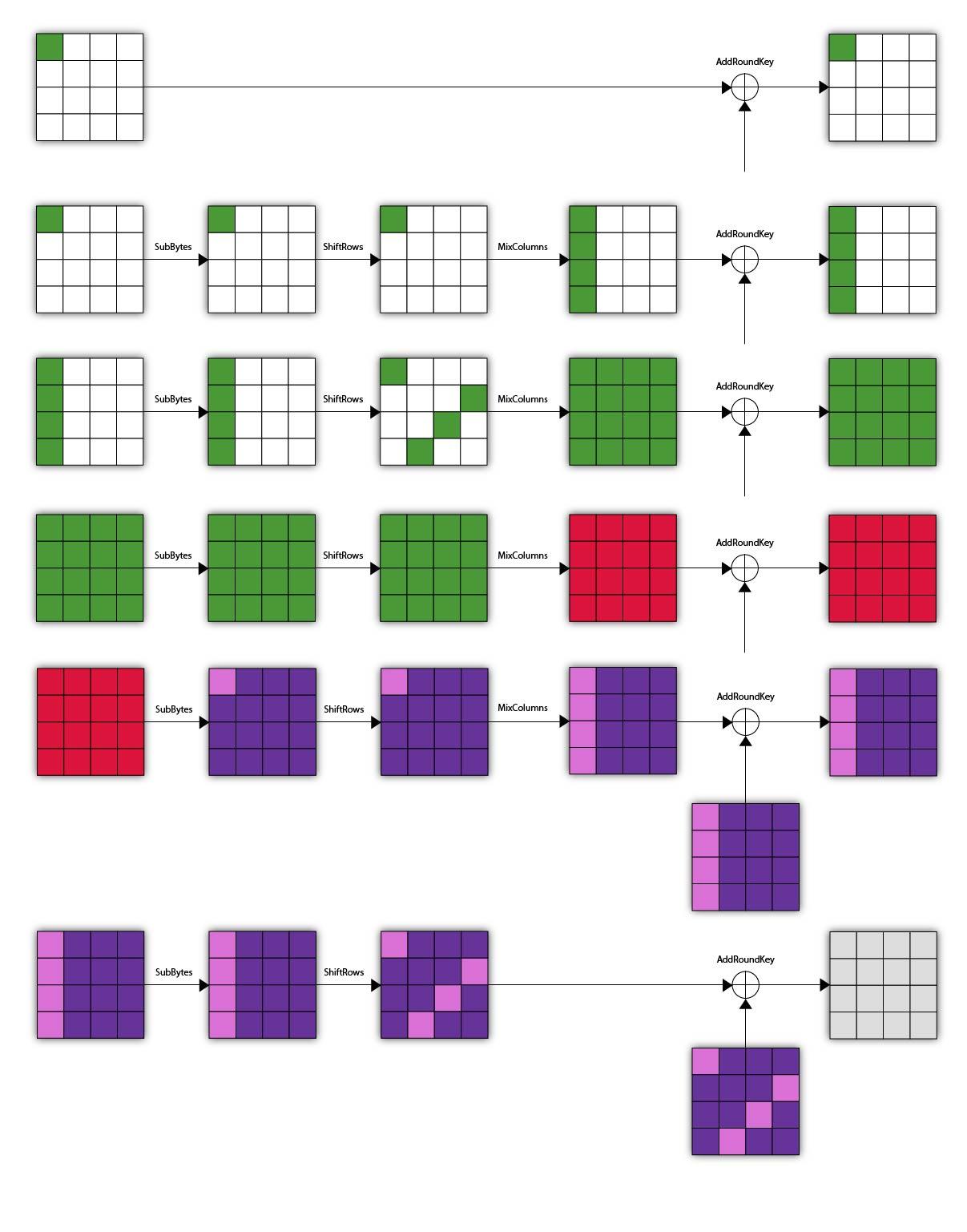
We still need the distinguisher, which means more effort to reverse the output backward to the point. Since there lies another mix_columns between the output and our target, we may have to recover 4 bytes of states in a group (bruteforcing 4 bytes of round_keys[-1]) at one time. The positions of the bytes are determined by shift_rows, as shown in the figure.
An interesting trick is that we can always swap mix_columns and add_round_key. In this way, we only need to bruteforce round_keys[-2] byte by byte (instead of in groups of 4). Then we can recover round_keys[-1] with the distinguisher.
The overall computational cost for a group of 4 keys is $\mathcal{O}(2^{40})$ (4+1 bytes). This is also highly parallelizable, thus leading to a $\mathcal{O}(k \cdot 2^{32})$. For implementation we may have to use cpp (or golang).
(*)it-hiding
This challenge is for speed-run on the second day.
In this challenge we need to solve a Pedersen Commitment decision problem.
Solution
Curve W25519 in this challenge is isomorphic to curve ed25519, with the curve order $8 \cdot q$. Since fastecdsa use a $q$-order generator $G$, an apparent solution is to integrate a point in another subgroup, thus changing the order of the commitment $C$. People can be inspired by the Schnorr part ig, which forces the user to send a point generated by $G$.
Consider we’re taking a 2-order point $B$, how can we by pass the Schnorr part? In Schnorr proof, we need to send $B, (z, c)$ satisfying $\operatorname{challenge}(z \cdot G-c \cdot B, B) = c$. Though we’re not able to predict $c$, we know the fact that $c \cdot B = O$ for any even $c$ (since $B$ is a 2-order point). Thus we can randomly pick $z$ for several times and compute $c = \operatorname{challenge}(z \cdot G, B)$, and we can successfully forge a valid proof $(z, c)$ when we get an even $c$. This may lead to a 50% success rate, acceptable.
One team used the time difference to do the decision, which seems to work locally. But I think this may be influenced badly by network delay and fastecdsa.
Yeah I didn’t manage to solve it in time, cuz I misused $8 \cdot q$ instead of $q$ while forging a proof, disappointment.
Milan -> Sardinia -> Rome
My first time to EU, fascinated.
Painful that I had to spend 30 hours on the plane, with bad sleep and endless plane food. But you always need to pay something ig.
 |
 |
|---|
My body arrived in Milan early in the morning (while my soul arrived after hours), and honestly the weather was very cold, gloomy and frustrating. But when we landed in Sardinia, things got better. I myself is kinda weather-sensitive so that was such a relief.
 |
 |
|---|
No so sure I had Linguine or Spaghetti that night.
 |
|---|
The CTF event’s just impressive. We really enjoyed all crypto challenges (it’d be better if we cleared them XD).
 |
 |
 |
|---|
I had to refresh myself from time to time because of jet lag, taking a glimpse of the local life. I may spend more days on the island next time, if possible.
 |
 |
 |
|---|
 |
|---|
The first night’s pizza was on the host, and I had Spaghetti and Macaroni on the second day.
Of courese I had things other than noodles lmao. It’s just fun trying to pick up different pastas.
 |
 |
|---|
 |
 |
|---|
Shouldn’t post the photo of them ig. But I think it’s a cool one XD
 |
|---|
We spent one day and a half in Rome after the event. Here comes Rome’s Day and Night.
I love pleasant weathers.
 |
 |
|---|
 |
 |
 |
|---|
 |
 |
|---|
 |
 |
|---|
A lemon🍋
 |
|---|
I had Fettuccine for my last meal before leaving. They’re all tasty, but noodles will not be an option for my next month ig.
 |
 |
 |
|---|