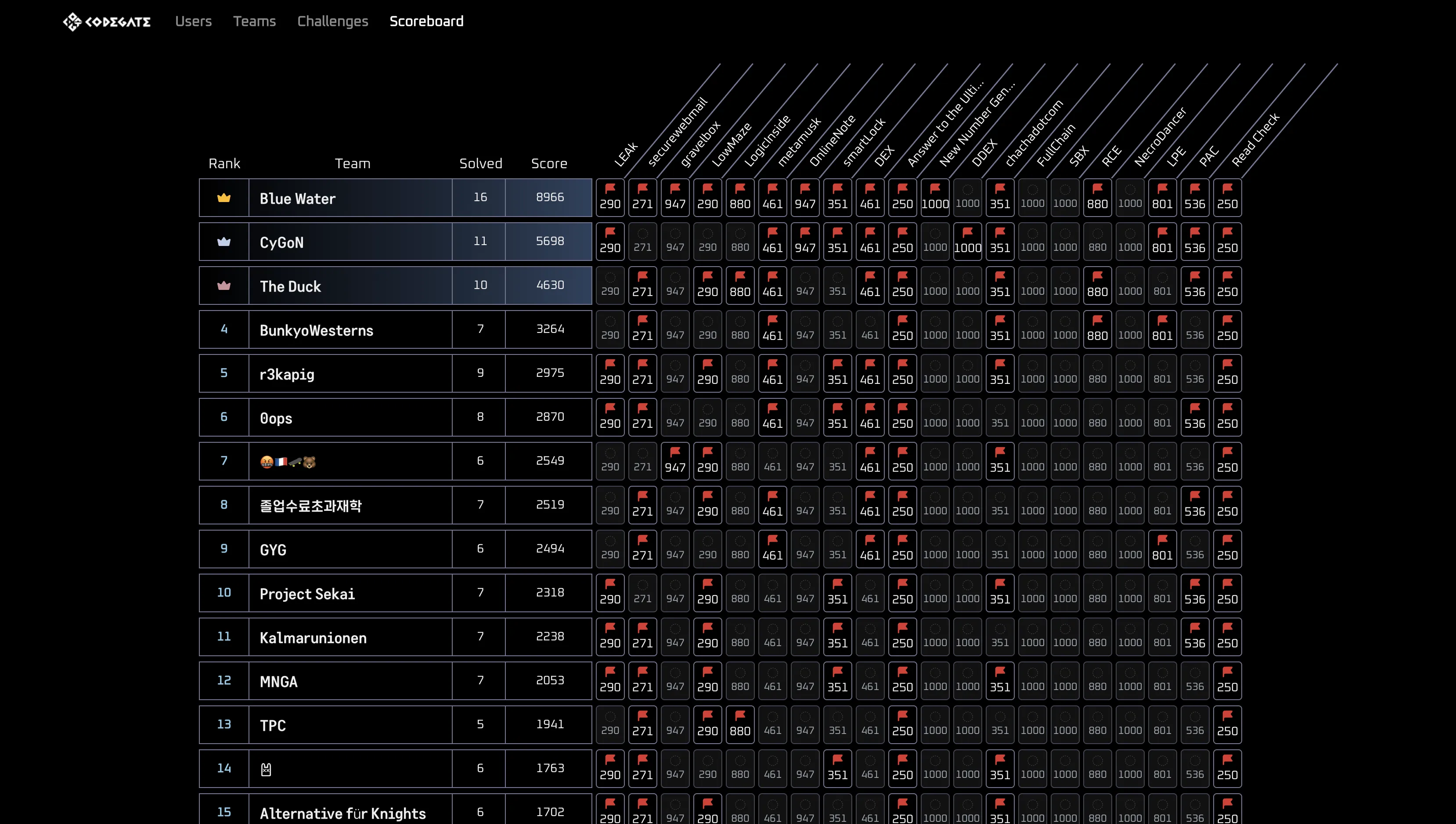
Time: 2025.07.10-11 (onsite)
I played Codegate CTF Final with r3kapig last week and we got 5th in the end.
Sincere thanks to my teammates and the organizers, I really enjoyed the game.
LEAk (12 solves)
This is a standard implementation of LEA, which is a ARX-style block cipher. Our target is to recover the key through 15 at maximum times of fault injection without the value of the fault.
And my solution is based on this.
The core of the attack is an algebraic representation of modular addition on $\mathbb{F}_{2^n}$. In short, we have the following equations if we try to inject a fault into the modular addition.
$$A \boxplus B = C \Rightarrow A \boxplus (B \oplus \Delta B) = C \oplus \Delta C$$
$$
\begin{cases}
c_0 = a_0 + b_0 \\
c_i = a_i + b_i + a_{i-1}b_{i-1} + (a_{i-1}+b_{i-1})(a_{i-1}+b_{i-1}+c_{i-1})\\
c_0+\Delta c_{0} = a_0 + b_0 + \Delta b_0 \\
c_i+\Delta c_{i} = a_i + b_i + \Delta b_i + a_{i-1}(b_{i-1}+\Delta b_{i-1}) + (a_{i-1}+b_{i-1}+\Delta b_{i-1})(a_{i-1}+b_{i-1}+\Delta b_{i-1}+c_{i-1})
\end{cases}
$$
With the knowledge of $(C, \Delta B, \Delta C)$, we can build a binary system with $2n$ variables, which can be solved through Groebner Basis or z3-solver. And we can recover the low $n-1$ bits of $(A, B)$ with enough samples (apparently we have no information about MSB).
In the second part we just need to choose the injection points, collect the outputs and recover the internal values using the above analysis. I implemented the paper’s strategy and here is a sketch.
- $\rightarrow X_{22}[0]$ for $RK_{23}[0]$ (31bit)
- $\rightarrow X_{23}[1]$ for $RK_{23}[1] \oplus RK_{23}[2]$ (31bit)
- $\rightarrow X_{23}[2]$ for $RK_{23}[3] \oplus RK_{23}[4]$ (31bit)
- $\rightarrow X_{22}[0]$ (reuse stage 1) for $RK_{23}[5]$ (30bit)
For more details you can check the original paper (and my exploit code). With some bruteforce on MSBs, we can recover the secret key.
In the paper the author takes 6 samples for each steps, and here we have only 5 (we need 1 sample for the original ciphertext). This slightly influences the success rate so we need several attempts.
It turns out the whole challenge is z3able but whatever :)
I actually enjoyed the implementation part, with snacks and classical music. Love and peace @codegate.
smartLock (10 solves)
A tiny bug is that the server checks the answer by sending $m^d \pmod{n}$ and querying $m$, so we can just pass all the tests with the public keys. This can be figured out through the remote outputs.
According to our REer, we may need to solve 10 ACDP in 50s with strict parameters. I’ve not tried it but it might be all about optimizations ig.
In Korea
Charming Seoul City. The weather is similar to that in my hometown.
Kinda hot in the first two days, but it’s just pleasant after that.
Glad to meet so many old and new friends :D
 |
 |
|---|