Time: 2025.03.01-02 (onsite)
I participated SECCON 13th Final as a member of P1G SEKAI this weekend, and we finally got 4th among international teams.
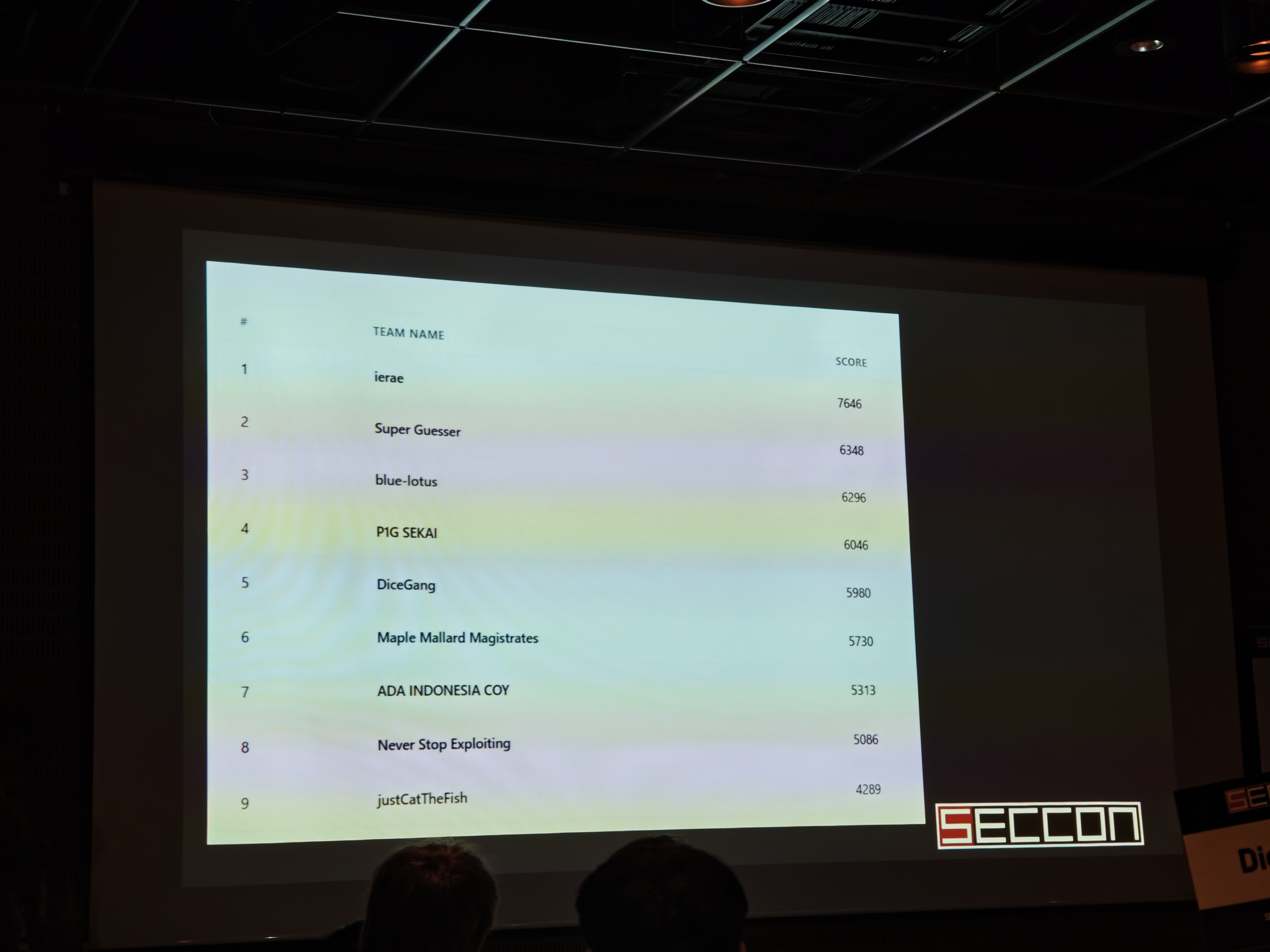
Nice crypto challenges, and I solved 3 out of 4. IF ONLY I’d ever taken some time to study UOV.
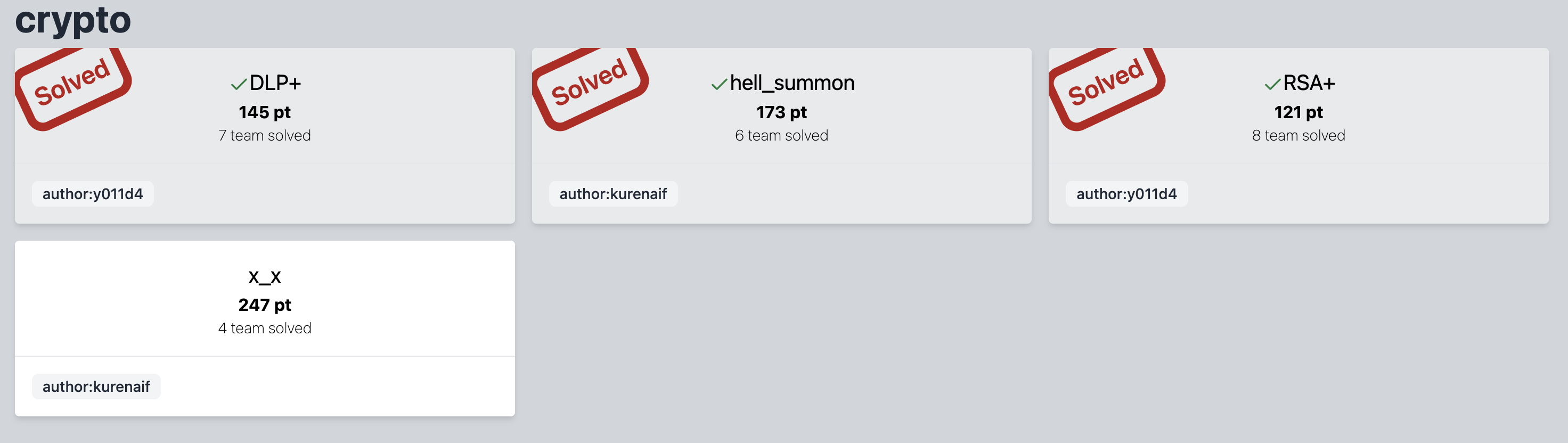
Or maybe I was just too nervous.
XO
RSA+ (8 solves)
It turns out that we can send two composite number $(p, q)$, both smaller than 512 bits. Then we can just find all the solutions on $p_i$ and combine them with CRT.
solution: exp.py
I believe there exists a better way though.
DLP+ (7 solves)
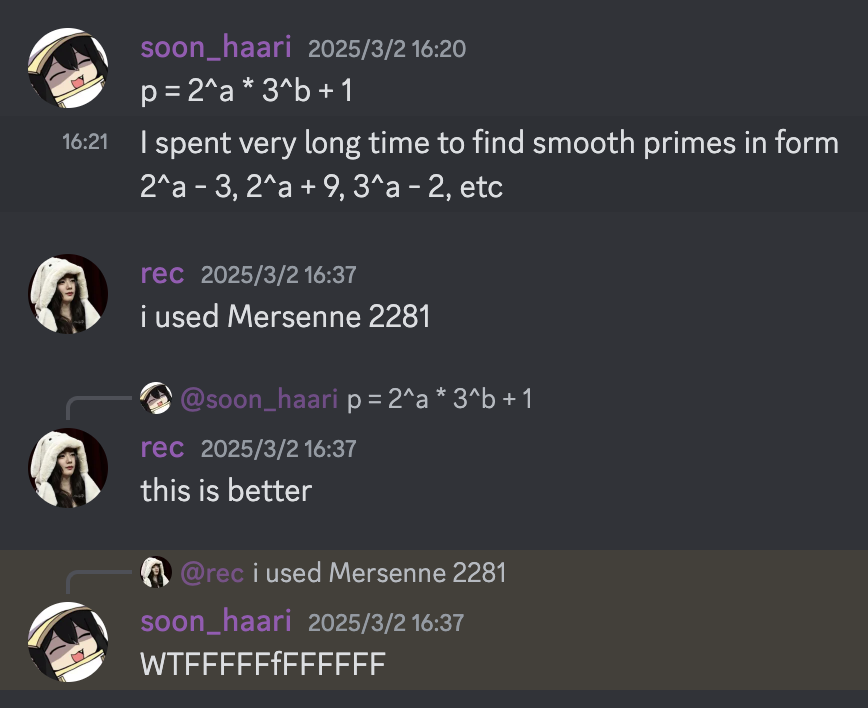
A simple idea is that we try to control $g^x$ (or $h^x$) to be small. Then we can get $h^x$ with some bruteforce and solve DLP to get $x$. I found some luck on Mersenne Prime $p = 2^n - 1$, where $g^x \pmod{p}$ is very small. Finally I chose M2281 for effective DLP solver.
Which took me a lot of time and luck, definitely NOT that effective.
solution: exp.py
@Sceleri and @soon_haari used $p = 2^a \cdot 3^b + 1$. It does make more sense since $g = 2^{a-1} \cdot 3^b$ and $h = 2^a \cdot 3^{b-1}$ (same in our solution). But I donot want to go through it again so just let it go.
hell_summon (6 solves)
I spent the whole afternoon day 1 on this one.
We have 42 pairs of $(m_i, c_i = r \cdot (m_i \oplus H) + e_i \pmod{p})$, where $e_i$ is due to the truncation. We rewrite $m_i \oplus H$ as $\Sigma_{j=0}^{39} (m_{i, j} + H_{j} - 2 \cdot m_{i, j} \cdot H_{j}) \cdot 2^{j}$.
$$\Rightarrow \Sigma_{j=0}^{39} r \cdot H_{j} \cdot ((1 - 2 \cdot m_{i, j}) \cdot 2^{j}) + r \cdot m_i + e_i \pmod{p}$$
Orthogonal Lattice seems to be an adorable choice, and it worked well. On the first attempt I found one short vector $v$ where $\vec{v} \cdot \vec{c} = \vec{v} \cdot \vec{e} \pmod{p}$, and it’s small enough to omit $p$. But I didn’t manage to solve $\vec{e}$.
On another attempt at midnight, I used vectors $(v_0, v_1)$ orthogonal to $\Sigma_{j=0}^{39} r \cdot H_{j} \cdot ((1 - 2 \cdot m_{i, j}) \cdot 2^{j})$. Then we have two equations $r \cdot (\vec{v_i} \cdot \vec{m}) + \vec{v_i} \cdot \vec{e} \pmod{p}$, where $\vec{v_i} \cdot \vec{e}$ is small. Now we can solve it as a simple HNP.
solution: exp.py
Definitely not a pleasing code but whatever.
*x_x (4 solves)
Working on it. UOV and sth bluhbluhbluh.
In Japan
My first time to Japan, also my first time abroad. Not bad actually.
 |
 |
 |
|---|
My teammates are very strong! Glad to work with them XD
And also great to meet many friends from P1G SEKAI.
 |
 |
|---|
Sincere thanks to @crazyman :D (Wish I could go to Mt. Fuji.)
I realy enjoyed Tokyo. It’d be better if I can hang out for one or two two more days.